Rumus GLBB (Gerak Lurus Berubah Beraturan) dan Contoh Soal
Sebelum mempelajari gerak lurus berubah beraturan, terlebih dahulu memahami apa itu percepatan. Karena ini saling berkaitan. Percepatan adalah hasil bagi perubahan kecepatan dengan selang waktu yang diperlukan untuk perubahan kecepatan.
Percepatan termasuk ke dalam besaran vektor. Artinya, selain memiliki nilai, tetapi juga memiliki arah. Percepatan dapat dirumuskan sebagai berikut:
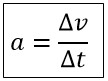
Keterangan:
- a = percepatan (m/s²)
- Δv = selisih kecepatan (m/s)
- Δt = selisih waktu (s)
Gerak lurus berubah beraturan (GLBB) adalah gerak lurus suatu benda yang kecepatannya berubah terhadap waktu akibat adanya percepatan yang tetap. Gerak lurus berubah beraturan dibedakan menjadi 2, yaitu:
1. Gerak lurus dipercepat beraturan
Hal ini terjadi bila kecepatan benda bertambah secara tertur. Rumus yang digunakan:

Sedangkan rumus yang digunakan untuk menghitung jarak gerak lurus dipercepat beraturan:

2. Gerak lurus diperlambat beraturan
Hal ini terjadi bila kecepatan benda berkurang secara teratur. Rumus yang digunakan:

Sedangkan rumus yang digunakan untuk menghitung jarak gerak lurus dipercepat beraturan:

Keterangan:
- vt = kecepatan setelah t (m/s)
- vo = kecepatan awal (m/s)
- a = percepatan (m/s²)
- t = waktu (s)
- s = jarak tempuh (m)
Untuk lebih memudahkan pemahaman tentang gerak lurus berubah beraturan, lihat contoh soal berikut:
Contoh Soal
Sebuah sepeda motor bergerak dengan kecepatan 10 m/s. Kemudian, setelah 7 detik kecepatannya berubah menjadi 16 m/s. Hitunglah percepatan dan jarak yang ditempuh oleh sepeda motor tersebut.
Diketahui:
vo = 10 m/s
t = 7 s
vt = 16 m/s
Ditanya: a (percepatan) dan s (jarak)?
Jawab:
a = vt-vo / Δt
= 16-10 / 7
= 7/6
= 1,16 m/s²
= 10 . 7 + ½ . 1,16 . 7²
= 70 + 28,42
= 98,42 m