Penjelasan Hukum Kirchhoff 1 dan 2 beserta Contoh Soalnya
Hukum Sirkuit Kirchhoff (Kirchhoffs Circuit Law) adalah aturan yang digunakan untuk memecahkan masalah rangkaian kompleks dengan mendefinisikan seperangkat hukum jaringan dasar dan teorema untuk tegangan dan arus di sirkuit.
Hukum Kirchhoff merupakan salah satu hal yang penting untuk dikuasai bagi orang yang berkecimpung di dunia teknik, khususnya teknik elektro.
Hukum Kirchhoff penggunaannya berkaitan erat dengan aturan persimpangan dan aturan loop tertutupnya.
Kita dapat menghitung dan menemukan arus juga tegangan di sekitar sirkuit tertutup, asalkan kita mengetahui nilai komponen listrik di dalamnya. Nilai komponen di sini yang dimaksud salah satunya adalah seperti besarnya hambatan.
Dalam menghitung besarnya nilai hambatan total atau resistansi total (RT), seperti ketika dua atau lebih resistor dihubungkan bersama dalam seri, paralel, atau kombinasi keduanya maka kita dapat dengan mudah mencari nilai hambatan total berdasarkan aturan Hukum Ohm.
Namun, terkadang dalam sebuah rangkaian yang kompleks, seperti jaringan atau sambungan T, kita tidak dapat hanya menggunakan Hukum Ohm saja untuk menemukan tegangan atau arus yang bersirkulasi di dalam rangkaian.
Untuk jenis perhitungan tersebut, kita memerlukan aturan tertentu yang memungkinkan memperoleh persamaan rangkaian. Oleh karena itu, dalam hal ini kita dapat menggunakan Hukum Rangkaian Kirchhoff.
Sedikit informasi mengenai awal mula hukum ini. Jadi, pada tahun 1845, seorang fisikawan Jerman, Gustav Kirchhoff membuat aturan atau hukum yang berkaitan dengan kekekalan arus dan energi dalam rangkaian listrik. Kedua aturan ini umumnya dikenal sebagai Hukum Sirkuit Kirchhoff.
Hukum pertama berkaitan dengan arus yang mengalir di sekitar sirkuit tertutup, dikenal sebagai Hukum Arus Kirchhoff atau Kirchhoffs Current Law (KCL).
Kemudian, hukum yang kedua berkaitan dengan tegangan yang ada di sirkuit tertutup, dikenal sebagai Hukum Tegangan Kirchhoff atau Kirchhoffs Voltage Law (KVL).
Baca Juga: Rumus Hukum Ohm dan Contoh Soalnya
Hukum Pertama Kirchhoff (Hukum Arus Kirchhoff)
Hukum Arus Kirchhoff menyatakan bahwa:
"total arus atau muatan yang memasuki titik percabangan sama persis dengan muatan yang meninggalkan titik percabangan”.
Dengan kata lain, jumlah dari semua arus yang masuk dan keluar dari suatu titik percabangan harus sama dengan nol, I(keluar) + I(masuk) = 0. Gagasan ini oleh Kirchhoff umumnya dikenal sebagai kekekalan muatan.
Pada gambar di atas terdapat titik percabangan dari lima jalur arus.
Kemudian, terdapat tiga arus yang memasuki titik percabangan, yaitu I1, I2, I3 di mana semuanya bernilai positif.
Sementara itu, terdapat dua arus yang meninggalkan titik percabangan, yaitu I4 dan I5 yang itu artinya bernilai negatif.
Dengan demikian, berarti kita dapat menulis ulang persamaannya menjadi: I1 + I2 + I3 – I4 – I5 = 0.
Hukum Kedua Kirchhoff (Hukum Tegangan Kirchhoff)
Hukum Tegangan Kirchhoff menyatakan bahwa:
"dalam rangkaian loop tertutup, tegangan total sama dengan jumlah semua penurunan tegangan dalam loop yang sama" yang juga sama dengan nol.
Dengan kata lain, jumlah dari semua tegangan dalam loop harus sama dengan nol. Gagasan Kirchhoff ini dikenal sebagai kekekalan energi.
Pada gambar di atas, ketika memulai perhitungan dari titik mana pun dalam loop, seterusnya lakukan ke arah yang sama, yaitu searah jarum jam atau berlawanan arah jarum jam, dan dengan memperhatikan arah semua penurunan tegangan, baik positif maupun negatif, hingga akhirnya kembali ke titik awal yang sama.
Kita dapat menggunakan hukum tegangan Kirchhoff saat menganalisis rangkaian seri.
Aturan Menentukan Tanda
Hukum kirchhoff digunakan pada sirkuit yang lebih kompleks, di mana tidak cukup hanya menggunakan hukum Ohm saja.
Langkah awal yang harus dipahami adalah menentukan di mana letak positif (+) dan negatif (–) di setiap komponen yang ada dalam sirkuit.
Untuk lebih jelasnya amati gambar di bawah.
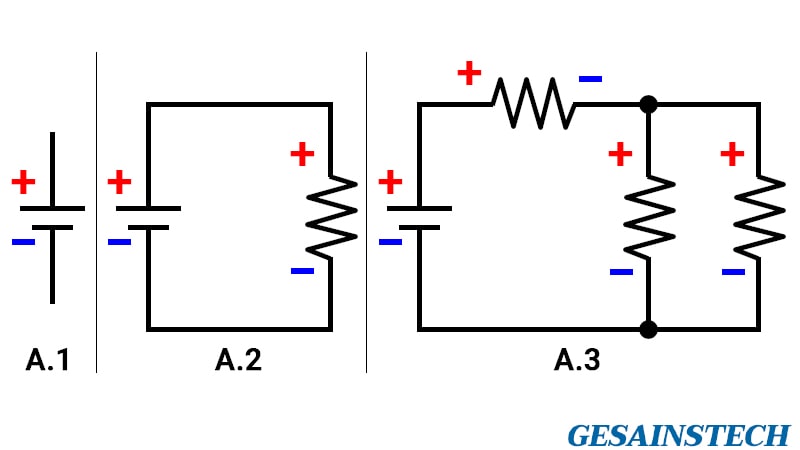
Pada gambar A.1 menunjukkan simbol sumber tegangan DC, di mana garis yang lebih panjang berarti positif dan yang pendek berarti negatif.
Kemudian, pada gambar A.2 sumber tegangan sudah dirangkai dengan satu resistor, di sini maka kaki/terminal resistor positif adalah yang langsung berhubungan dengan positif sumber tegangan, begitu juga untuk yang negatif.
Pada gambar A.3 adalah rangkaian yang lebih kompleks daripada A.2, tetapi konsep pemberian tandanya sama.
Apabila sudah paham dalam hal pemberian tanda +/– pada komponen, selanjutnya mengetahui arah loop untuk perhitungan.
Arah arus listrik adalah dari potensial tinggi ke potensial rendah, atau dari positif ke negatif.
Kemudian, arah dari loop terdapat dua, yaitu searah jarum jam dan berlawanan arah jarum jam.
Artinya, jika arah loop searah dengan arah arus listrik maka nilainya akan menjadi negatif (–), karena ini sama saja seperti (loop) melewati dari potensial tinggi ke potensial rendah sehingga terjadi penurunan tegangan (negatif).
Bagaimana jika loop berlawanan dengan arah arus listrik? Nilainya akan menjadi positif (+). Itu karena (loop) melawati dari potensial rendah ke potensial tinggi sehingga tegangan meningkat.
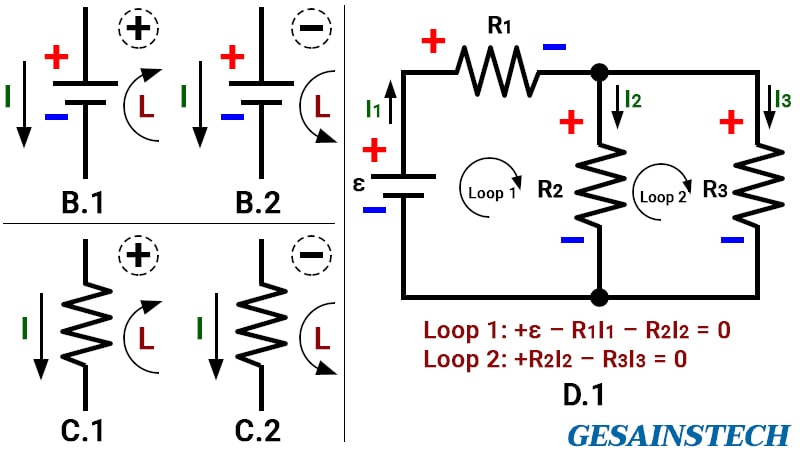
Untuk lebih memahami amati gambar di atas. Pada gambar B.1 arah loop dari potensial rendah ke potensial tinggi sehingga tegangan meningkat maka nilai ggl baterai positif, sedangkan gambar B.2 adalah sebaliknya.
Kemudian, amati gambar C.1 di situ arah loop berlawanan dengan arah arus listrik atau dari potensial rendah ke potensial tinggi sehingga tegangan meningkat maka resistor bernilai positif, sedangkan C.2 adalah kebalikannya.
Amati gambar D.1 yang merupakan rangkaian tertutup dan terdapat dua loop yang arahnya searah jarum jam semua.
Pada loop satu maka persamaannya adalah +ε – R1I1 – R2I2 = 0. Kemudian, pada loop dua persamaannya adalah +R2I2 – R3I3 = 0.
Namun, jika kedua loop diubah menjadi berlawanan arah jarum jam maka persamaannya, yaitu loop 1: –ε + R2I2 + R1I1 = 0, sedangkan loop 2: –R2I2 + R3I3 = 0.
Baca Juga: Teorema Thevenin dan Cara Perhitungan Rangkaian
Contoh Soal
Untuk membantu Anda agar lebih memahami lagi tentang hukum Kirchhoff, di bawah sudah tersedia beberapa contoh soal beserta jawabannya yang dapat dipelajari.
Soal No.1
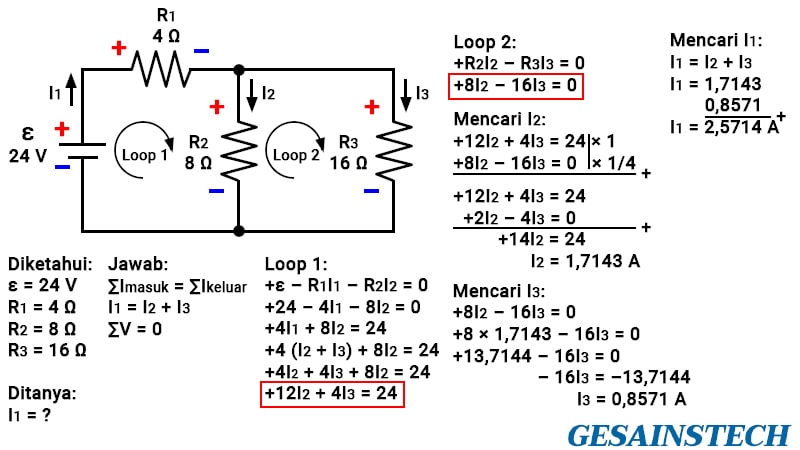
Pada soal gambar di atas terdapat tiga buah resistor yang dirangkai secara seri-paralel, sementara sumber tegangan (DC) memiliki GGL sebesar 24 V.
Kemudian, yang ditanyakan adalah berapa besarnya I1.
Jadi, untuk mengetahui besarnya arus di setiap cabang (I1, I2, dan I3) dapat menggunakan cara eliminasi kemudian substitusi.
Jawaban dari soal tersebut ternyata untuk I1 = 2,5714 A, I2 = 1,7143 A, dan I3 = 0,8571.
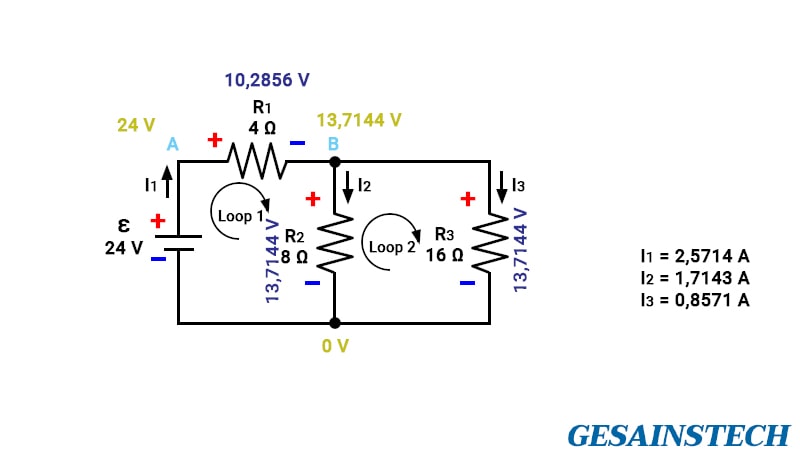
Setelah itu, untuk mengetahui apakah jawabannya sesuai atau masuk akal maka perlu dilakukan analisis pada rangkaian.
Pada rangkaian di atas arus I1 adalah penjumlahan atau gabungan dari I2 dan I3. Kemudian, lanjut untuk menganalisa tegangannya.
Sebelumnya asumsikan terlebih dahulu titik 0V di mana akan dijadikan titik referensi.
Selanjutnya, jumlahkan setiap beda potensial atau tegangan di setiap loop, dengan menggunakan aturan yang sudah dijelaskan sebelumnya.
Dalam loop 1: +ε – R1I1 – R2I2 = 0 menjadi +24 – 4×2,5714 – 8×1,7143 = 0 menjadi +24 – 10,2856 – 13,7144 = 0.
Kemudian, untuk loop 2: +R2I2 – R3I3 = 0 menjadi +8×1,7143 – 16×0,8571 = 0 menjadi +13,714 – 13,714 = 0.
Soal No.2
Soal kedua mencari besarnya arus I1, I2, dan I1–I3. Namun, soal kedua ini memiliki dua sumber tegangan, di mana besarnya tegangan atau ggl, yaitu ε1 30 V dan ε2 20 V.
Di sini pasti akan timbul pertanyaan, ke mana arus listrik akan mengalir?
Dalam hal ini penting untuk diingat bahwa arus listrik mengalir dari potensial tinggi ke potensial rendah. Jadi, arus akan mengalir dari ε1. Namun, bahkan apabila Anda salah dalam menganalisa, maksudnya salah dalam menebak aliran arus maka arusnya menjadi negatif, bukan positif.
Jadi, jika demikian, Anda hanya perlu membalikkan anak panah (arah arus) dari arah sebelumnya sehingga akan menjadi positif.
Jika Anda mengamati gambar rangkaian pada soal, di situ arus I3 tidak ditulis, melainkan diganti dengan I1–I2. Mengapa demikian?
Sebelumnya, amati dahulu dua rangkaian (berwarna hijau) di kanan atas. Di situ pada rangkaian yang atas, arah arus ditulis menjadi lima variabel (I1, I2, I3, I4, dan I5).
Kelemahannya adalah kita membutuhkan lima persamaan untuk menyelesaikan lima variabel yang hilang.
Namun, kita dapat menyederhanakan prosesnya seperti gambar rangkaian bawah karena hanya memiliki tiga variabel, bukan lima.
Jadi, mengapa gambar rangkain pada soal ditulis I1–I2, bukan I3? Jawabannya tentu saja untuk menyederhanakan ketika dikerjakan.
Untuk analisa rangkaian soal nomor 2, Anda dapat mencermati gambar di bawah.
Dalam menganalisa soal nomor 2, arus I1 adalah gabungan dari I2 dan I1–I2.
Untuk mencari tegangan pada setiap resistor gunakan hukum Ohm, yaitu besarnya arus yang mengalir dikalikan besarnya hambatan resistor.
Kemudian, Anda dapat dengan mudah mengetahui besarnya tegangan dari suatu titik ke titik referensi 0 V.
Soal No.3
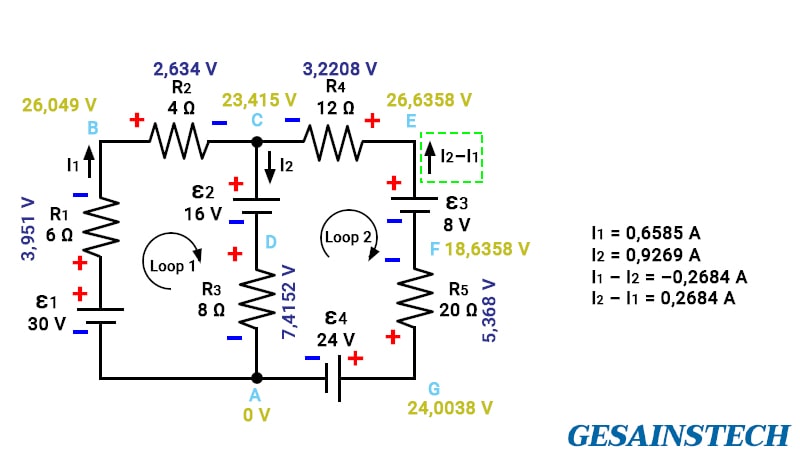
Soal ketiga ini memiliki empat sumber tegangan, di mana terdapat kesulitan tersendiri ketika menentukan arah arus. Namun, arus listrik akan selalu mengalir dari potensial tinggi ke potensial rendah.
Jadi, pada rangkaian di atas dapat di asumsikan bahwa arus mengalir dari ε1 30 V.
Kemudian, langkah selanjutnya menganalisa arah aliran arus.
Setelah dikerjakan I1 hasilnya positif, yaitu 0,6585. Artinya, arah arus dari I1 satu benar karena hasilnya positif, atau bukan negatif. Namun, apabila I1 hasilnya negatif, berarti arah arus mengalir sebaliknya.
Kemudian, untuk I2 hasilnya juga positif, yaitu 0,9269 sehingga arah arus dari I2 juga benar.
Akan tetapi, arah arus dari I1–I2 hasilnya adalah negatif –0,2684 ini artinya arah arusnya salah.
Oleh karena itu, ganti dengan I2–I1 di mana jawabannya positif 0,2684 dan arah arus diubah dari arah berlawanan dari yang sebelumnya, tanda +/– pada resistor juga diubah (lihat gambar di bawah).
Dalam menganalisa soal nomor 3 yang cukup membingungkan adalah arus pada I1–I2 ketika dalam persamaan hasilnya negatif.
Artinya, arus tersebut salah dalam asumsi sebelumnya. Maka dari itu yang benar adalah I2–I1 sehingga hasilnya diperoleh 0,2684.
Untuk mencari kebenarannya, kita harus ingat bahwa arus yang keluar sama dengan arus yang masuk. Dengan demikian, I2 adalah penjumlahan atau gabungan dari I1 dan I2–I1, yaitu 0,6585 + 0,2684 = 0,9269 A.
Soal No.4
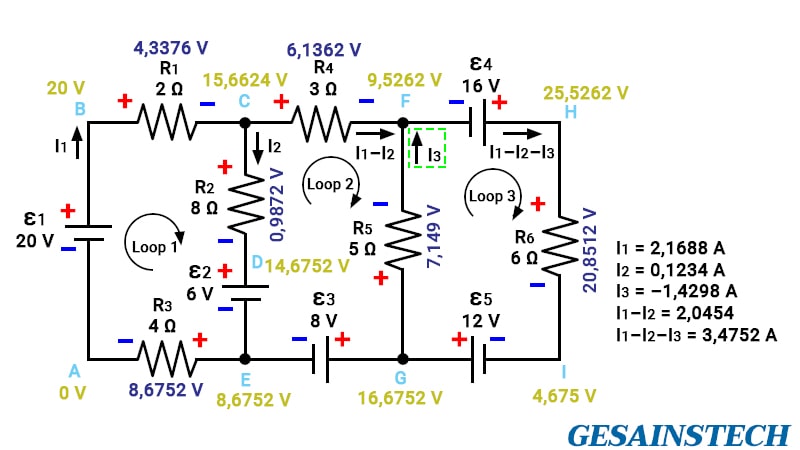
Rangkaian di atas memiliki tiga loop. Artinya, pengerjaannya juga lebih kompleks.
Untuk pengerjaanya cari dahulu tegangan yang paling tinggi, di sini adalah ε1 20V.
Kemudian, asumsikan jika arus mengalir dari ε1, nanti jika ada arah yang salah maka hasilnya negatif.
Dalam mengerjakan persamaan pada loop 1, untuk menghitung tegangan pada R3 adalah dikalikan dengan I1.
Langkah berikutnya adalah menganalisa rangkaian.
Hasilnya adalah I1 dan I2 memiliki nilai yang positif, sedangkan I3 negatif. Artinya, arah arus I3 berlawanan dengan yang sudah diasumsikan sebelumnya.
Untuk bukti pembenarannya, dapat dihitung dari tegangan pada titik G dikurangi dengan tegangan titik F dan selanjutnya dibagi dengan R5, yang mana hasilnya adalah +1,4298 A.
Kemudian, hasil dari persamaan I3 adalah negatif, yang mana ketika dimasukkan dalam persamaan I1–I2–I3 = 3,4752 A.
Sebelumnya kita tahu bahwa dalam hukum Kirchhoff arus yang masuk sama dengan arus yang keluar. Dengan kata lain arus pada I1–I2–I3 adalah penjumlahan daripada I3 dan I1–I2 yang mana hasilnya sama 3,4752 A. Jadi, hasil dalam persamaan I3 = –1,4298 adalah benar.