Hukum Kirchhoff 2: Bunyi, Rumus, dan Contoh Soal
Hukum Kirchhoff 2 biasa disebut sebagai Hukum Tegangan Kirchhoff atau Kirchhoff’s Voltage Law (KVL) adalah hukum kedua Kirchhoff yang berhubungan dengan kekekalan energi di sekitar jalur sirkuit tertutup.
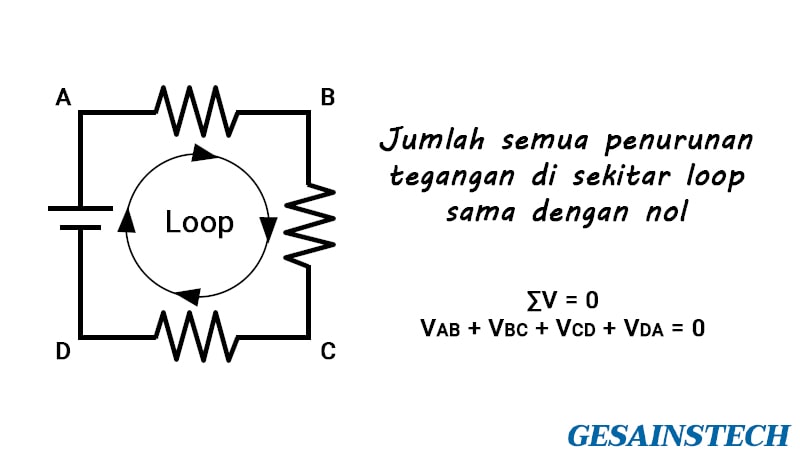
Hukum tegangan Kirchhoff adalah yang kedua dari hukum dasarnya yang dapat digunakan untuk analisis rangkaian. Hukum tegangan Kirchhoff menyatakan bahwa:
"dalam sirkuit loop tertutup, tegangan total sama dengan jumlah semua penurunan tegangan dalam loop yang sama" yang juga sama dengan nol. Dengan kata lain, jumlah dari semua tegangan dalam loop harus sama dengan nol, atau ΣV = 0.
Gagasan oleh Kirchhoff ini umumnya dikenal sebagai kekekalan energi, karena bergerak di sekitar loop tertutup atau sirkuit tertutup.
Anda akan kembali ke tempat Anda memulai di sirkuit dan karenanya kembali ke potensi awal yang sama tanpa kehilangan tegangan di sekitar sirkuit, seperti halnya siklus yang melingkar.
Oleh karena itu, setiap penurunan tegangan di sekitar loop harus sama dengan sumber tegangan yang ditemui di sepanjang jalur.
Jadi, ketika menerapkan hukum tegangan Kirchhoff ke elemen rangkaian tertentu, penting bagi kita untuk memberikan perhatian khusus pada tanda positif (+) dan negatif (–) dari penurunan tegangan pada elemen dan ggl sumber. Jika tidak maka perhitungan kita mungkin salah.
Baca Juga: Hukum Kirchhoff 1: Bunyi, Rumus, dan Contoh Soal
Aturan Menentukan Tanda
Dalam menganalisis sirkuit yang lebih kompleks, hukum Ohm saja tidak cukup. Maka dari itu, menggunakan hukum Kirchhoff adalah aturan yang dapat diandalkan dalam sirkuit yang lebih kompleks.
Langkah awal yang harus dipahami adalah menentukan di mana letak positif (+) dan negatif (–) di setiap komponen yang ada dalam sirkuit. Untuk lebih jelasnya amati gambar di bawah ini.
Pada gambar A.1 menunjukkan simbol sumber tegangan DC, di mana garis yang lebih panjang berarti + dan yang pendek berarti —.
Kemudian, pada gambar A.2 sumber tegangan sudah dirangkai dengan satu resistor, di sini maka kaki/terminal resistor + adalah yang langsung berhubungan dengan + sumber tegangan, begitu juga untuk yang negatif.
Pada gambar A.3 adalah rangkaian yang lebih kompleks daripada A.2, tetapi konsep pemberian tandanya sama.
Langkah selanjutnya mengetahui arah loop untuk perhitungan.
Arah arus listrik adalah dari potensial tinggi ke potensial rendah, atau dari positif (+) ke negatif (—).
Kemudian, arah dari loop terdapat dua, searah jarum jam dan berlawanan arah jarum jam. Artinya, jika arah loop searah dengan arah arus listrik maka nilainya akan menjadi negatif (–), karena ini sama saja seperti (loop) melewati dari potensial tinggi ke potensial rendah sehingga terjadi penurunan tegangan (negatif).
Bagaimana jika loop berlawanan dengan arah arus listrik? Nilainya akan menjadi positif (+). Itu karena (loop) melawati dari potensial rendah ke potensial tinggi sehingga tegangan meningkat.
Pada gambar B.1 arah loop dari potensial rendah ke potensial tinggi sehingga tegangan meningkat maka nilai ggl baterai positif, sedangkan gambar B.2 adalah sebaliknya.
Kemudian, amati gambar C.1 di situ arah loop berlawanan dengan arah arus listrik atau dari potensial rendah ke potensial tinggi sehingga tegangan meningkat maka resistor bernilai positif, sedangkan C.2 adalah kebalikan dari C.1.
Selanjutnya, pada gambar D.1 yang merupakan rangkaian tertutup dan terdapat dua loop yang arahnya searah jarum jam semua. Pada loop 1 maka persamaannya adalah +ε – R1I1 – R2I2 = 0. Kemudian, pada loop 2 persamaannya adalah +R2I2 – R3I3 = 0.
Namun, jika kedua loop diubah menjadi berlawanan arah jarum jam maka persamaannya menjadi loop 1: –ε + R2I2 + R1I1 = 0, sedangkan loop 2: –R2I2 + R3I3 = 0.
Baca Juga: Rumus Hukum Ohm dan Contoh Soalnya
Contoh Soal
Hukum Kirchhoff menjadi lebih mudah dipahami apabila melihat atau mencoba langsung soal-soal. Maka dari itu, di bawah sudah disediakan beberapa contoh soal dan jawaban beserta penjelasannya, di mana Anda dapat mencermatinya langsung.
Soal No.1
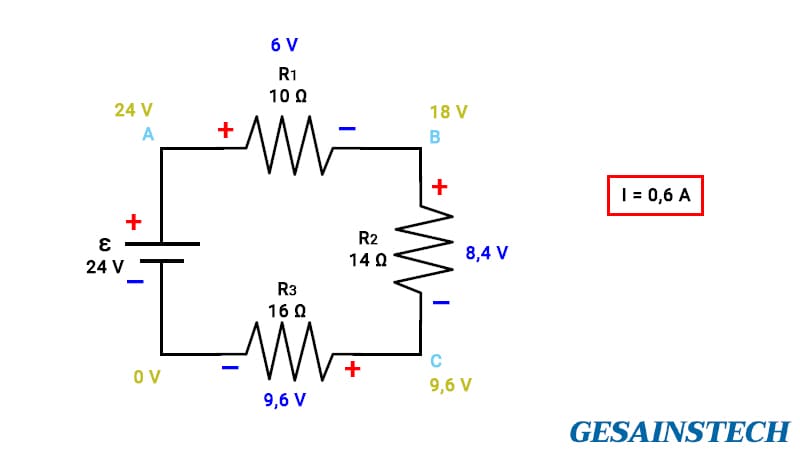
Pada soal nomor 1 di atas, terdapat tiga buah resistor yang dirangkai secara seri dengan sumber tegangan (DC) yang memiliki GGL sebesar 24 V.
Kemudian, yang ditanyakan adalah berapa besarnya I (arus). Ini karena dengan mengetahui besarnya arus yang mengalir maka dapat digunakan untuk menghitung besarnya setiap penurunan tegangan, di mana setiap penurunan tegangan dalam sirkuit tertutup jika seluruhnya dijumlahkan maka hasilnya 0. Jawaban dari soal tersebut ternyata untuk I = 0,6 A.
Setelah itu, untuk mengetahui apakah jawabannya sesuai atau masuk akal maka perlu dilakukan analisis pada rangkaian.
Besarnya arus yang sudah diketahui dapat digunakan untuk menghitung penurunan tegangan di setiap resistor dengan aturan hukum Ohm, V = I × R.
Untuk memudahkan menganalisa, dalam sirkuit dapat diberi titik/poin penurunan tegangan, pada sirkuit di atas terdapat titik A, B, C dan 0 V sebagai referensi.
Titik A 24 V. Titik B adalah hasil dari titik A dikurangi tegangan pada R1, yaitu 18 V. Titik C merupakan hasil dari pengurangan titik B dan tegangan R2, yaitu 9,6 V. Sementara itu, hasil pengurangan titik C dan tegangan R3 adalah 0 V.
Jadi, jika semua penurunan tegangan dijumlahkan maka hasilnya akan 0 V.
Baca Juga: Rumus Rangkaian Pembagi Tegangan dan Contoh Soal
Soal No.2
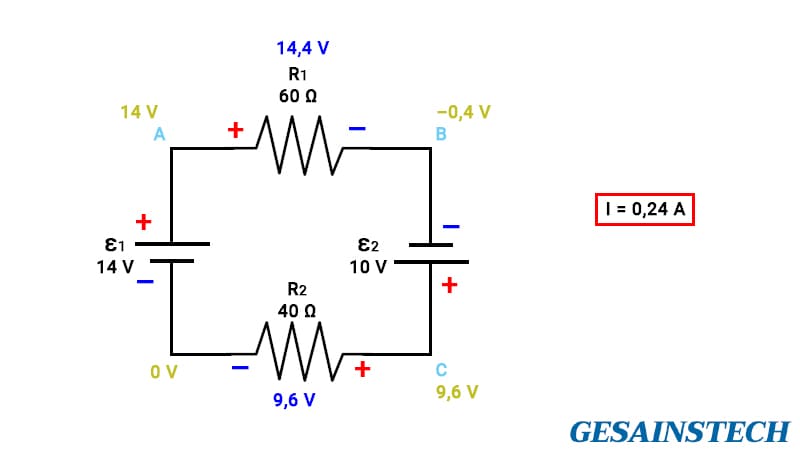
Soal nomor 2, terdapat 2 sumber tegangan dan 2 resistor. Mengerjakan jenis soal yang seperti ini penting untuk diketahui bahwa arus listrik mengalir dari potensial tinggi ke potensial rendah.
Jadi, karena terdapat 2 sumber ggl yang mana tidak saling bertentangan, dalam artian kedua sumber tersebut arah arusnya searah.
Sementara itu, arah dari loop yang dipakai juga searah jarum jam maka persamaannya dapat ditulis +ε1 – R1I + ε2 – R2I = 0. Jawabannya adalah I = 0,24 A.
Selanjutnya, menganalisa di dalam sirkuit.
Titik A 14 V. Titik B adalah hasil dari titik A dikurangi tegangan pada R1, yaitu –0,4 V. Titik C merupakan hasil dari penjumlahan titik B dan tegangan ε2, yaitu –0,4 + 10 = 9,6 V. Sementara itu, hasil pengurangan titik C dan tegangan R2 adalah 0 V.
Jadi, jika semua penurunan tegangan dijumlahkan maka hasilnya akan 0 V.
Soal No.3
Soal nomor 3 tiga, terdapat tiga sumber tegangan, di mana ε1 arah arusnya searah jarum jam, sedangkan ε2 dan ε3 berlawanan dengan arah jarum jam.
Untuk menentukan arah arus dari sirkuit tertutup adalah berpegang pada aturan arus listrik bergerak dari potensial tinggi ke potensial rendah.
Jadi, karena tegangan ε1 lebih besar, bahkan apabila tegangan ε2 dan ε3 digabungkan, maka arus mengalir dari ε1.
Dengan demikian, persamaannya adalah +ε1 – R1I – ε2 – ε3 – R3I = 0. Jawabannya adalah I = 0,5 A. Selanjutnya, menganalisa di dalam sirkuit.
Titik A 70 V. Titik B adalah hasil dari titik A dikurangi tegangan pada R1, yaitu 60 V. Titik C merupakan hasil dari penjumlahan titik B dan tegangan ε2, yaitu 60 + (–25) = 35 V. Sementara itu, hasil penjumlahan titik C dengan ε3 dan tegangan R2 adalah 35 + (–15) + (–20) = 0 V.
Jadi, jika semua penurunan tegangan dijumlahkan maka hasilnya akan 0 V.