Rangkaian Kapasitor Seri dan Paralel beserta Contoh Soal
Kapasitor adalah perangkat elektronika yang mampu menyimpan energi dalam bentuk muatan listrik. Dibandingkan dengan baterai dengan ukuran yang sama, kapasitor dapat menyimpan energi dalam jumlah yang jauh lebih kecil, sekitar 10.000 kali lebih kecil, tetapi cukup berguna untuk banyak desain sirkuit.
Kapasitor terbuat dari dua plat logam, dipisahkan oleh bahan isolasi yang disebut dielektrik. Plat bersifat konduktif dan biasanya terbuat dari aluminium, tantalum, atau logam lainnya, sedangkan dielektrik dapat dibuat dari segala jenis bahan isolasi, seperti kertas, kaca, keramik atau apapun yang dapat menghalangi aliran arus.
Kapasitor dapat dihubungkan secara seri atau paralel, di mana itu ditujukan untuk mendapatkan nilai resultan yang dapat berupa jumlah dari nilai individu (paralel) atau nilai kurang dari kapasitansi terkecil (seri).
Rangkaian Seri Kapasitor
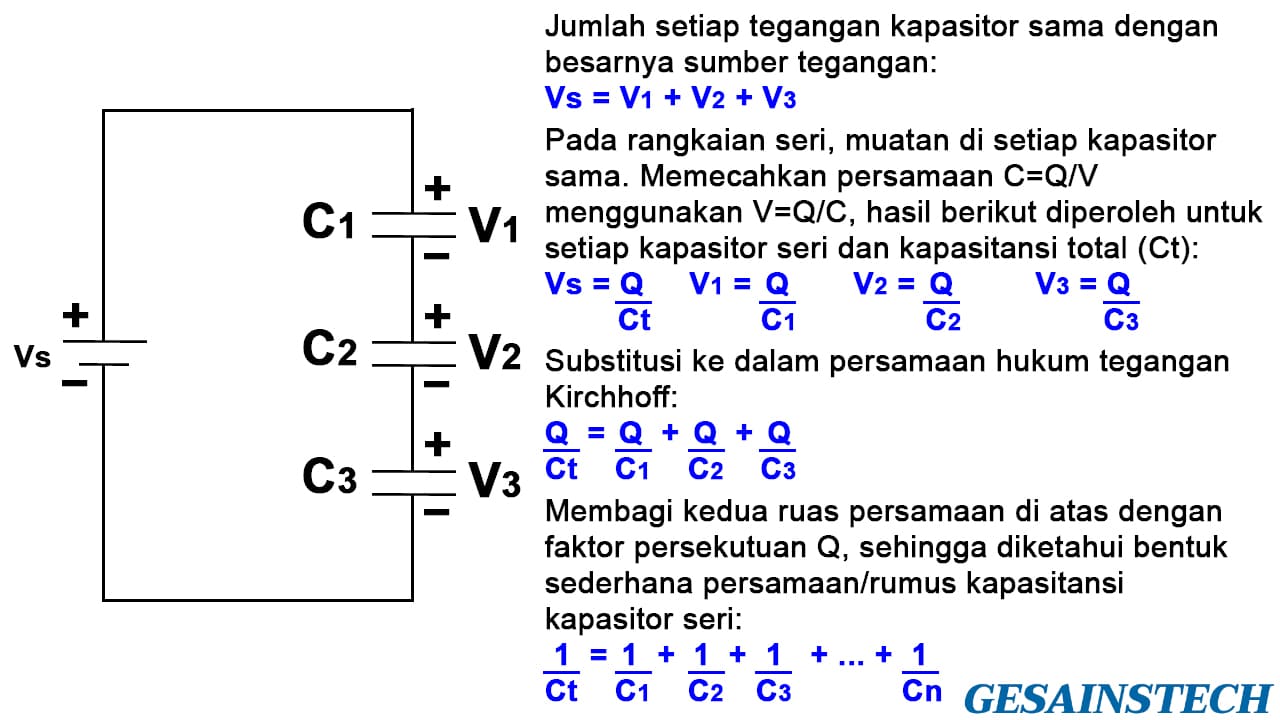
Ketika kapasitor dirangkai seri, perpindahan arus yang mengalir melalui setiap kapasitor dalam rangkaian adalah sama, sedangkan tegangan yang diberikan (tegangan sumber) akan dibagi di setiap individu kapasitor. Gambar di bawah menunjukkan rangkaian yang terdapat sumber tegangan dan tiga kapasitor dirangkai seri.
Pada saat dirangkai secara seri, jumlah tegangan dari setiap kapasitor harus sama dengan tegangan sumber (Vs), sesuai dengan hukum tegangan Kirchhoff.
Muatan (Q) pada semua kapasitor harus sama, karena kapasitor dihubungkan secara seri dan setiap pergerakan muatan di satu komponen harus terjadi di semua komponen rangkaian seri.
Kemudian, untuk mengetahui besarnya kapasitansi total (Ct) maka dapat menggunakan persamaan C = Q / V untuk tegangan dalam hal kapasitansi dan muatan (V = Q / C). Lebih jelasnya Anda dapat mengamati pada gambar di atas, di mana akhirnya diketahui persamaan atau rumus untuk menghitung kapasitansi total pada kapasitor yang dirangkai seri adalah 1/Ct = 1/C1 + 1/C2 + 1/C3 +...+ 1/Cn.
Dengan demikian, sudah jelas dari rumus di atas bahwa kapasitansi total kapasitor yang dirangkai secara seri kurang dari kapasitansi kapasitor individu mana pun.
Rangkaian Paralel Kapasitor
Ketika kapasitor dihubungkan secara paralel, satu plat dari setiap kapasitor dihubungkan langsung ke salah satu terminal sumber, sedangkan plat lainnya dari setiap kapasitor dihubungkan ke terminal sumber yang lain.
Amati gambar di bawah, semua plat negatif kapasitor dihubungkan bersama, dan semua plat positif dihubungkan bersama. Kapasitansi adalah fungsi langsung dari luas plat. Menghubungkan kapasitor secara paralel maka secara efektif meningkatkan luas plat sehingga meningkatkan kapasitansi total.
Kapasitor yang dirangkai paralel, kapasitansi totalnya dapat dihitung secara matematis, yaitu dengan menerapkan persamaan C = Q / V ke setiap kapasitor dan ke kapasitansi total. Sementara itu, muatan total (Qt) adalah jumlah muatan pada masing-masing kapasitor. Lebih jelasnya Anda dapat mengamati pada gambar di atas, di mana akhirnya diketahui persamaan atau rumus untuk menghitung kapasitansi total pada kapasitor yang dirangkai paralel adalah Ct = C1 + C2 + C3 +...+ Cn.
Dengan demikian, dari persamaan atau rumus di atas menyatakan secara matematis bahwa total kapasitansi dari sejumlah kapasitor yang dirangkai secara paralel adalah jumlah dari masing-masing kapasitansi kapasitor.
Baca Juga: Teori Dasar dan Cara Kerja Kapasitor
Contoh Soal
Untuk memudahkan pemahaman Anda, di bawah ini sudah tersedia beberapa contoh soal yang dapat Anda cermati.
Soal no.1
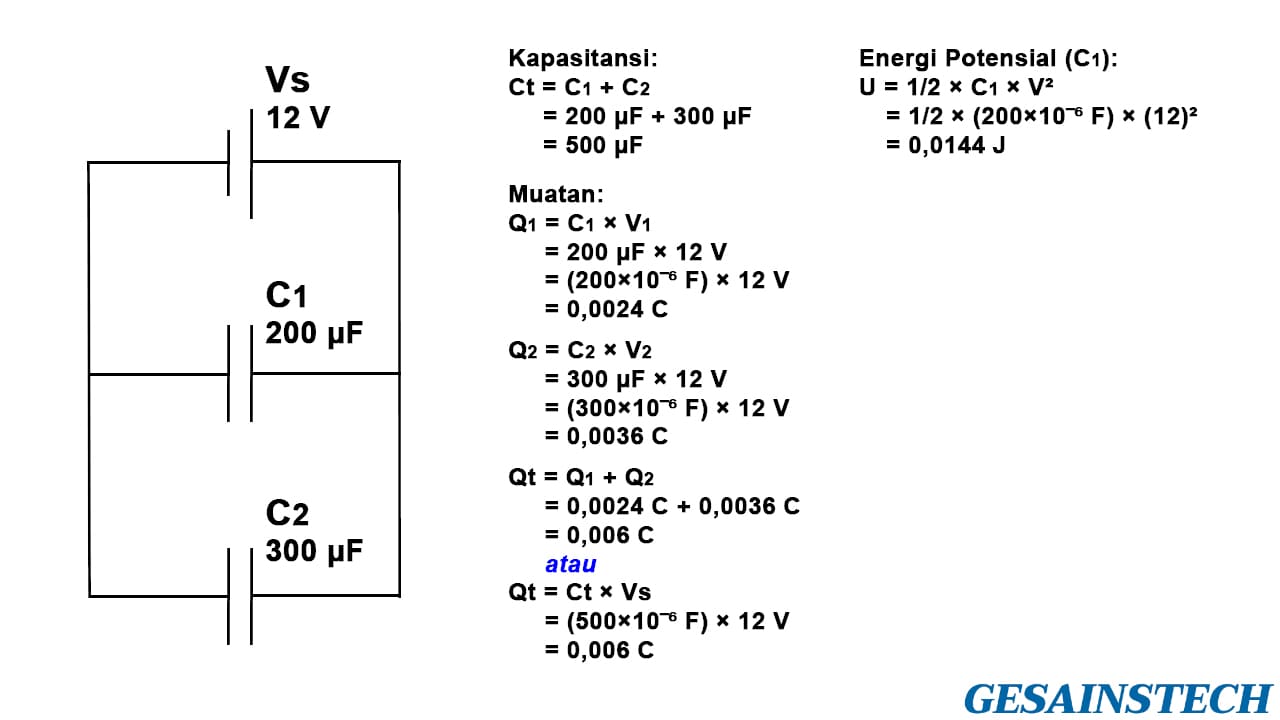
Terdapat dua kapasitor (C1 dan C2) yang dirangkai secara paralel, di mana sumber tegangannya (Vs) sebesar 12 V. Hitunglah total kapasitansi, besarnya muatan total, dan energi potensial listrik di C1.
Pertama hitung dahulu total kapasitansi (Ct) dari penjumlahan kedua kapasitor tersebut, karena disusun secara paralel maka cukup dijumlahkan secara sederhana saja, dan jawabannya adalah 500 µF.
Kemudian, mencari besarnya muatan, karena dirangkai secara paralel maka besarnya tegangan di setiap kapasitor sama dengan sumber tegangan (Vs). Selanjutnya, hitung muatan dengan rumus Q = C × V sehingga diketahui Q1 = 0,0024 C dan Q2 = 0,0036 C. Sementara itu, untuk mencari muatan total (Qt) dapat dengan cara menjumlahkan Q1 dan Q2 atau kapasitansi total dikali sumber tegangan, jawabannya 0,006 C.
Terakhir mencari besarnya energi potensial listrik yang tersimpan di dalam kapasitor C1. Anda dapat menggunakan persamaan atau rumus U = 1/2 × C × V². Oleh karena yang dicari energi potensial listrik di C1 maka persamaannya U = 1/2 × C1 × V², dan jawabannya adalah 0,0144 J.
Soal no.2
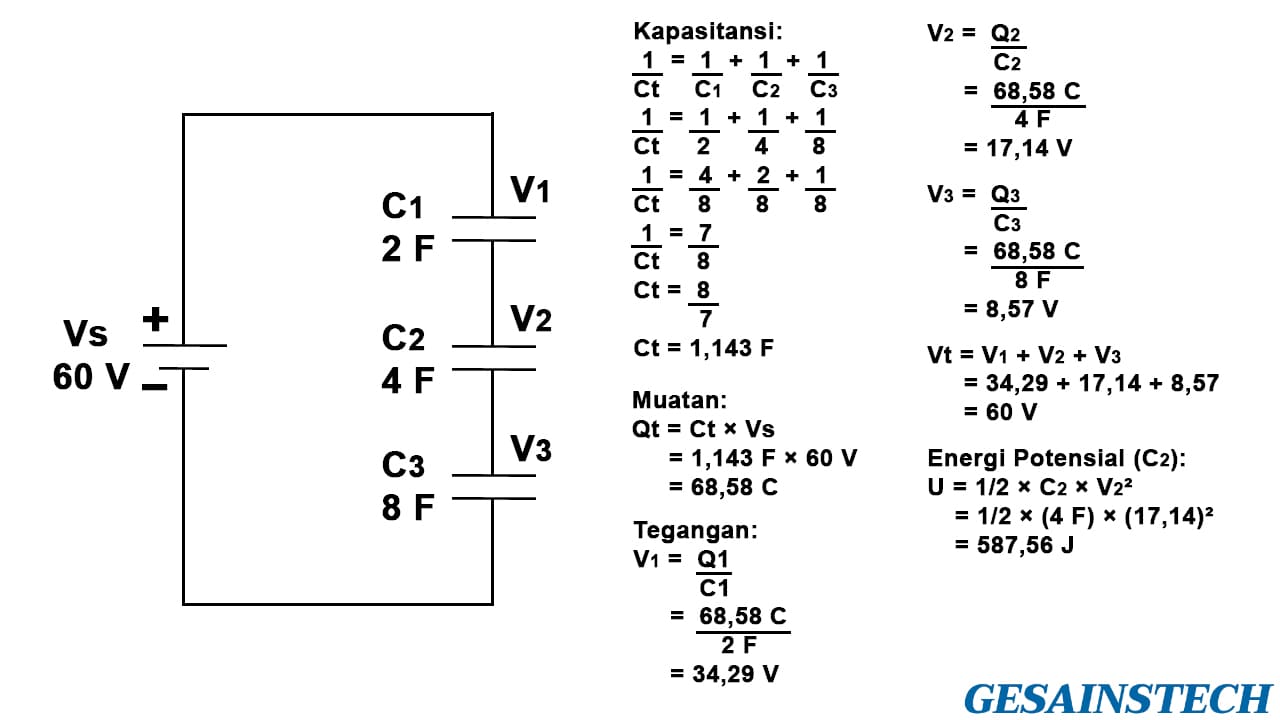
Terdapat tiga kapasitor C1 = 2 F, C2 = 4 F, dan C3 = 8 F (lihat gambar di bawah) yang dirangkai secara seri, di mana sumber tegangannya (Vs) sebesar 60 V. Hitunglah total kapasitansi, besarnya muatan total, tegangan di setiap kapasitor, dan energi potensial listrik di C2.
Kapasitansi total (Ct) kapasitor dalam rangkaian seri dapat dihitung menggunakan persamaan atau rumus 1/Ct = 1/C1 + 1/C2 + 1/C3 +...+ 1/Cn. Jawabannya adalah 1,143 F.
Selanjutnya, hitung besarnya muatan. Sebelumnya perlu diketahui bahwa pada kapasitor yang dirangkai seri besarnya muatan yang tersimpan di setiap kapasitor adalah sama. Jadi, untuk persamaannya dapat ditulis muatan total (Qt) sama dengan kapasitansi total (Ct) dikali sumber tegangan (Vs), hasilnya adalah 68,58 C.
Kemudian, hitung besarnya tegangan di setiap kapasitor. Pada rangkaian paralel besarnya tegangan di setiap kapasitor adalah sama dengan sumber tegangan. Namun, pada rangkaian seri tegangan di setiap kapasitor akan berbeda jika nilai kapasitansinya berbeda, atau dapat juga diartikan tegangan yang diberikan (tegangan sumber) akan dibagi di setiap individu kapasitor. Selanjutnya, untuk mencari tegangan Anda dapat menggunakan persamaan V = Q / C sehingga diketahui V1 = 34,29 V, V2 = 17,14 V, dan V3 = 8,57 V. Untuk memastikannya Anda dapat menjumlahkannya menjadi tegangan total (Vt), di mana hasilnya Vt = Vs.
Terakhir mencari besarnya energi potensial listrik yang tersimpan di dalam kapasitor C2. Anda dapat menggunakan persamaan atau rumus U = 1/2 × C2 × V² dan jawabannya adalah 587,56 J.
Soal no.3
Terdapat empat kapasitor C1 = 5 µF, C2 = 20 µF, C3 = 10 µF, dan C4 = 15 µF (lihat gambar di bawah) yang dirangkai secara seri-paralel, di mana sumber tegangannya (Vs) sebesar 80 V. Hitunglah total kapasitansi, besarnya muatan total, tegangan di setiap kapasitor, dan energi potensial listrik.
Sebelum menghitung kapasitansi total (Ct) Anda terlebih dahulu menyederhanakan atau meringkas dengan mengerjakan rangkaian paralel dahulu, yaitu kapasitor C2 dan C3, di mana nilai kapasitansi C23 = 30 µF. Kemudian, cari kapasitansi total dengan menjumlahkan C1, C23, dan C4 hasilnya adalah 3,75 µF.
Dalam mencari muatan penting untuk diketahui di rangkaian seri setiap muatan kapasitor sama, sedangkan rangkaian paralel setiap muatan kapasitor berbeda. Jadi, Anda dapat asumsikan C1, C23, dan C4 dirangkai secara seri sehingga muatannya sama, 300 µC atau 0,0003 C. Namun, C23 adalah gabungan dari dua kapasitor, Anda dapat mencari muatan C2 dengan persamaan Q2 = Qt × (C2 / C2+C3) jawabannya 200 µC, sedangkan C3 persamaannya Q3 = Qt × (C3 / C2+C3) jawabannya 100 µC.
Besarnya tegangan akan sama ketika dirangkai paralel, dan berbeda saat dirangkai seri. Jadi, C1, C23, dan C4 yang dirangkai seri maka jika dijumlahkan hasilnya akan sama dengan sumber tegangan. Oleh karena C2 dan C3 dirangkai paralel maka nilai tegangannya sama.
Soal no.4
Terdapat empat kapasitor C1 = 40 µF, C2 = 140 µF, C3 = 25 µF, dan C4 = 100 µF (lihat gambar di bawah) yang dirangkai secara seri-paralel, di mana sumber tegangannya (Vs) sebesar 100 V. Hitunglah total kapasitansi, besarnya muatan total, tegangan di setiap kapasitor, dan energi potensial listrik.
Pertama menyederhanakan dahulu rangkaian sehingga memudahkan dalam mencari kapasitansi. Cari kapasitansi C34, yaitu dengan menjumlahkan C3 dan C4. Selanjutnya, jumlahkan C2 dan C34 sehingga diketahui C234. Terakhir cari kapasitansi total dengan menjumlahkan C1 dan C234.
Anda dapat mencari muatan total dengan mengalikan kapasitansi total dan tegangan sumber, di mana muatan total (Qt) sama dengan muatan C1 (Q1). Kemudian, cari muatan C2 (Q2). Untuk muatan C3 (Q3) dan muatan C4 (Q4) nilainya sama karena seri. Apabila dijumlahkan Q3 dan Q2 maka hasilnya akan sama dengan Q1 atau Qt.
Tegangan pada C3 (V3) dan C4 (V4) jika dijumlahkan maka hasilnya akan sama pada tegangan C2 (V2). Sementara itu, V2 dan V1 jika dijumlahkan maka hasilnya akan sama dengan tegangan sumber (Vs).
Soal no.5
Terdapat lima kapasitor C1 = 400 µF, C2 = 60 µF, C3 = 80 µF, C4 = 240 µF dan C5 = 120 µF (lihat gambar di bawah) yang dirangkai secara seri-paralel, di mana sumber tegangannya (Vs) sebesar 200 V. Hitunglah total kapasitansi, besarnya muatan total, tegangan di setiap kapasitor, dan energi potensial listrik.
Jumlahkan dahulu kapasitor seri C345 (C3, C4, dan C5) hasilnya jumlahkan lagi dengan kapasitor paralel C2 menjadi C2345. Kemudian, cari kapasitansi total dengan menjumlahkan C1 dan C2345.
Muatan Qt = Q1. Sementara itu, Q3 = Q4 = Q5. Kemudian, jika Q2 + Q3 = Q1.
Tegangan V2 = V3 + V4 + V5. Kemudian, V2 + V1 = Vs. Setiap tegangan pada loop jika Anda jumlahkan sesuai dengan hukum tegangan Kirchhoff ∑V = 0 maka hasilnya akan 0.