Pengosongan Kapasitor Konstanta Waktu Rangkaian RC
Sebelumnya telah dibahas tentang bagaimana teori pengisian kapasitor konstanta waktu rangkaian RC. Selanjutnya, pada artikel ini akan dibahas kebalikannya, yaitu teori tentang bagaimana pengosongan kapasitor dalam rangkaian RC (resistor-kapasitor) menggunakan konstanta waktu rangkaian RC.
Kapasitor dikatakan dalam keadaan terisi penuh ketika mencapai 5 konstanta waktu atau dikenal dengan 5T. Pada saat kapasitor terisi penuh dan kemudian kapasitor diputus dari sumber tegangannya (baterai), maka energi yang tersimpan selama proses pengisian akan tetap berada di platnya (dengan syarat kapasitor masih dalam keadaan baik dan mengabaikan kehilangan internal).
Namun, jika baterai diganti dengan short circuits, ketika saklar ditutup (close) maka kapasitor akan melakukan pengosongan. Proses pengosongan ini akan berhenti setelah kedua plat kapasitor memiliki muatan (proton dan elektron) yang sama atau menjadi netral.
Kapasitor melakukan pengosongan tidak dengan cara yang konstan, di mana pada kondisi awal t = 0, i = 0 dan q = Q. Kemudian, untuk tegangan kapasitor pada awal pengosongan adalah sama dengan tegangan sumber atau dapat ditulis Vc = Vs. Ini karena pada saat t = 0 tegangan kapasitor berada di puncaknya, begitu juga arus pengosongan kapasitor.
Baca Juga: Cara Kerja Kapasitor dan Teori Dasar
Kurva Pengosongan Rangkaian RC
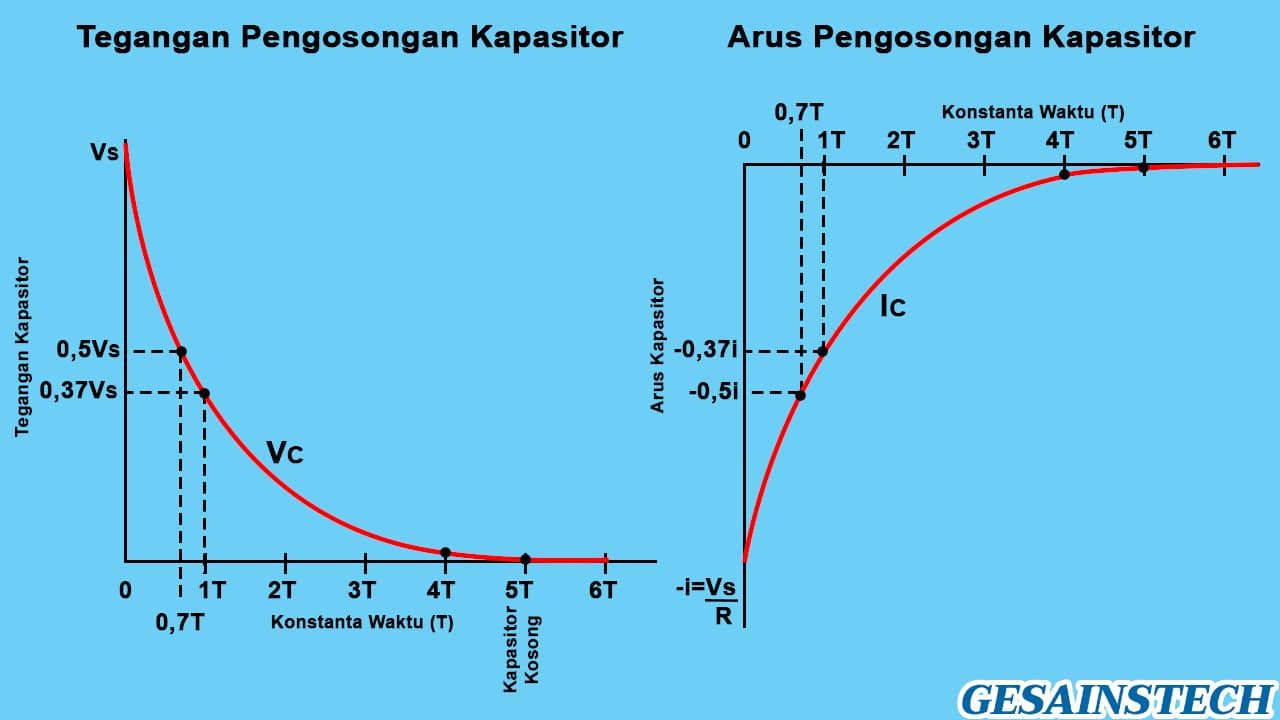
Amati gambar kurva tegangan dan arus di atas. Pada saat awal pengosongan, kurva tingkat proses pengosongan kapasitor terlihat lebih curam, tetapi kemudian berkurang secara eksponensial karena kapasitor kehilangan muatan pada tingkat yang lebih lambat. Dengan adanya pengosongan membuat tegangan kapasitor berkurang sehingga arus pemakaian juga ikut berkurang, tanda negatif hanya berarti arah arus berlawanan dengan arah pengisian (charging).
Pada pengosongan kapasitor rangkaian RC, nilai konstanta waktu masih sama dengan nilai 63%. Kemudian, karena awalnya kapasitor terisi penuh, selanjutnya terjadi pengosongan sehingga tegangan turun menjadi 63% dari nilai awlanya, yaitu 1 – 0,63 = 0,37 atau 37% dari nilai akhirnya.
Maka dari itu, konstanta waktu menunjukkan sebagai waktu yang dibutuhkan kapasitor untuk melepaskan hingga 63% dari nilai terisi penuh. Dengan demikian, satu kali konstanta waktu untuk rangkaian pengosongan RC menunjukkan sebagai tegangan plat yang mewakili 37% dari nilai akhirnya (nilai akhirnya adalah menjadi nol volt atau habis sepenuhnya).
Pengosongan Konstanta Waktu Rangkaian RC
Bilangan Euler (e) adalah bilangan irasional yang bernilai 2,718281828… dst. Bilangan ini dinamakan dari penemunya, yaitu Leonhard Euler, seorang ahli matematika dari Swiss.
Sama seperti pengisian kapasitor, dalam pengosongan kapasitor juga terdapat konstanta waktu. Ini karena konstanta waktu adalah ukuran seberapa cepat pengisian atau pengosongan.
Tabel Pengosongan Rangkaian RC
Anda dapat mengamati kurva dan tabel pengosongan rangkaian RC, di mana proses pengosongannya tidak linier, melainkan eksponensial. Oleh karena itu, supaya lebih memudahkan dan atau untuk tujuan yang lebih praktis, setelah lima konstanta waktu (5T), tegangan kapasitor jauh lebih kecil dari 1%, dalam hal ini kapasitor sudah dianggap sepenuhnya habis.
Contoh Soal
No.1
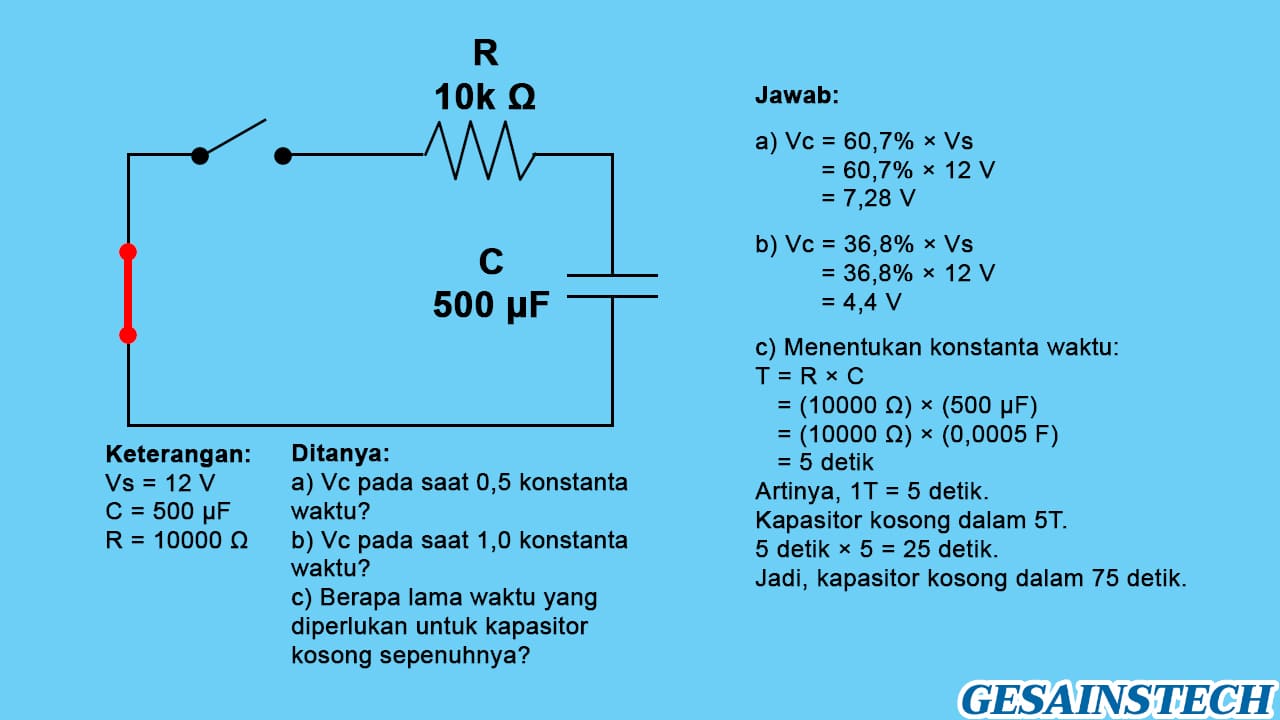
Dalam rangkaian pengosongan RC, terdapat sebuah resistor 10k Ω, dan kapasitor 500 µF terisi penuh hingga 12 V. Kemudian, pada kapasitor dilakukan pengosongan. Hitung konstanta waktu RC, T dari rangkaian pengosongan RC berikut ketika pertama kali saklar ditutup (close): Vc pada saat 0,5 konstanta waktu, Vc pada saat 1,0 konstanta waktu, dan yang terakhir berapa waktu yang dibutuhkan untuk kapasitor kosong sepenuhnya.
No.2
Pada rangkaian pengosongan RC, terdapat sebuah resistor 10k Ω, dan kapasitor 400 µF yang terisi penuh hingga 12 V. Kemudian, pada kapasitor dilakukan pengosongan. Hitung konstanta waktu, Vc pada saat 3,0 konstanta waktu, dan Vc pada 10 detik.
Terima kasih sudah membaca :)