Teorema Norton dan Cara Perhitungan Rangkaian
Teorema Norton adalah metode analitik yang digunakan untuk mengubah rangkaian yang kompleks menjadi rangkaian ekuivalen sederhana yang terdiri dari satu resistansi yang diparalelkan dengan sumber arus.
Teorema Norton menyatakan bahwa “Setiap rangkaian linier yang terdiri dari beberapa sumber energi dan resistansi dapat digantikan dengan generator arus konstan tunggal secara paralel dengan resistor tunggal.”
Rangkaian listrik baru hasil dari aplikasi teorema Norton disebut dengan sirkuit ekuivalen Norton. Nama dari teorema ini diambil dari penemunya yang bernama E. L. Norton beliau adalah seorang insinyur yang dahulu pernah bekerja di Bell Telephone Laboratories.
Teorema Norton mirip dengan teorema Thevenin. Dengan demikian, memungkinkan untuk menyederhanakan rangkaian linier apapun menjadi rangkaian ekuivalen. Namun, alih-alih menggunakan sumber tegangan dan resistansi seri, rangkaian ekuivalen Norton terdiri dari sumber arus dengan resistansi paralel. Menerapkan teorema Norton untuk menyederhanakan rangkaian dapat membuatnya lebih mudah untuk mengevaluasi beban variabel.
Baca Juga: Penjelasan Hukum Kirchhoff 1 dan 2 beserta Contoh Soalnya
Sama seperti teorema Thevenin dan teorema superposisi, teorema Norton terbatas untuk digunakan dengan rangkaian linier, di mana semua persamaan yang mendasarinya tidak termasuk eksponen atau akar. Sebuah rangkaian linier adalah yang menggunakan komponen pasif standar, seperti resistor, induktor, dan kapasitor. Selain itu, juga menggunakan sumber tegangan, seperti baterai dan sumber arus.
Sama halnya dengan teorema Thevenin, semua yang ada di rangkaian asli, kecuali resistansi beban dapat direduksi menjadi rangkaian ekuivalen yang lebih mudah dianalisis. Selain itu, seperti juga dalam teorema Thevenin, langkah-langkah yang digunakan dalam teorema Norton untuk menghitung arus sumber Norton (I-Norton) dan resistansi Norton (R-Norton) umumnya akan serupa.
Cara Menggunakan Teorema Norton
Teorema Norton menyatakan bahwa semua rangkaian linier dapat disederhanakan menjadi rangkaian ekuivalen dengan sumber arus tunggal secara paralel dengan resistor tunggal yang dihubungkan ke beban. Berikut adalah langkah-langkah untuk menentukan sirkuit ekuivalen Norton:
- Lepas resistor beban dan ganti dengan short circuit (hubung singkat).
- Hitung arus Norton, yaitu arus yang melalui short circuit.
- Ganti sumber daya. Semua sumber tegangan diganti dengan short circuit, dan semua sumber arus diganti dengan sirkuit terbuka (open circuit).
- Hitung resistansi Norton, yaitu resistansi antara titik sambungan rangkaian terbuka setelah semua sumber dilepas.
- Gambar rangkaian ekuivalen Norton dengan sumber arus Norton paralel dengan resistansi Norton. Resistor beban dipasang kembali di antara dua titik terbuka rangkaian ekuivalen.
- Terakhir, analisis tegangan dan arus untuk beban mengikuti aturan untuk rangkaian paralel.
Contoh Menentukan Rangkaian Ekuivalen Norton
Selanjutnya, untuk lebih memudahkan pemahaman tentang teorema Norton, di sini akan diberikan contoh langkah-langkah bagaimana cara menentukan rangkaian ekuivalen Norton (arus Norton dan resistansi Norton).
1. Lepas resistor beban dan ganti dengan short circuit.
2. Hitung arus Norton
Untuk menemukan besarnya arus Norton (untuk sumber arus di rangkaian ekuivalen Norton), lakukan penyambungan jalur/kabel secara langsung (short circuit atau hubung singkat) antara titik beban dan tentukan arus yang dihasilkan.
Perhatikan bahwa langkah-langkah di sini berlawanan dengan langkah-langkah dalam teorema Thevenin, di mana ketika resistor beban dilepas (menjadi rangkaian terbuka) dan kemudian menghitung tegangan.
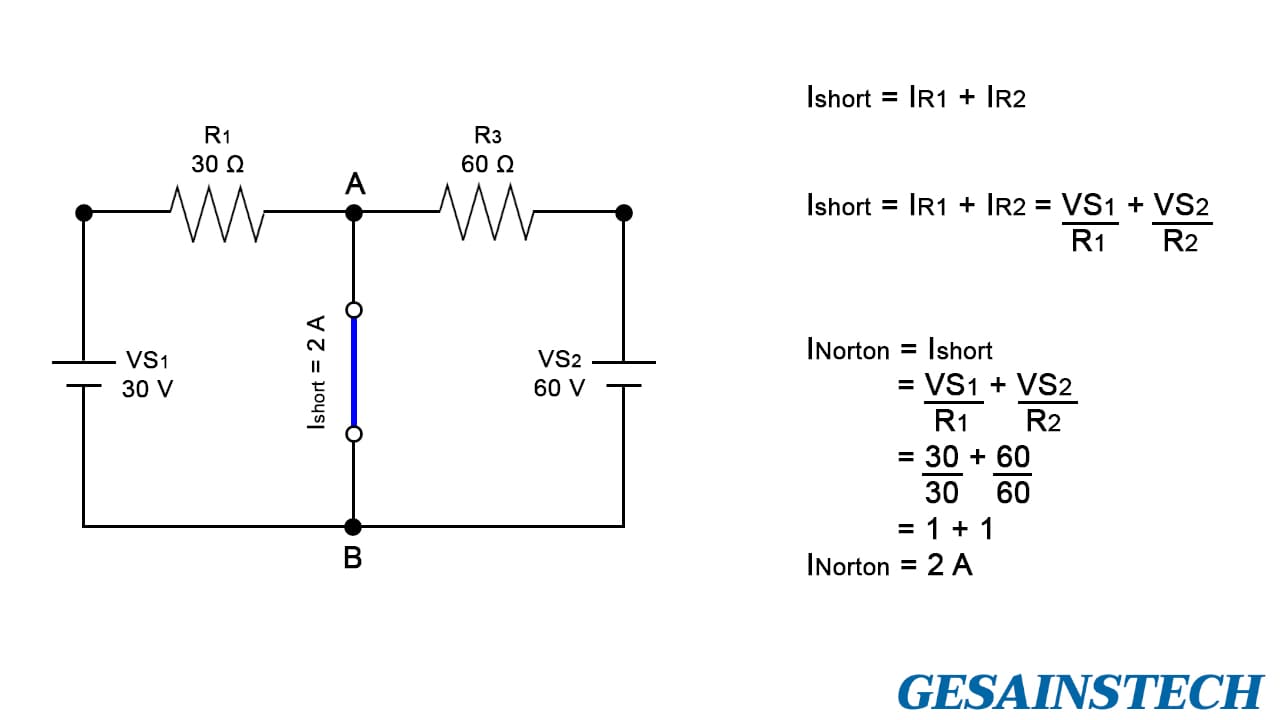
Setelah itu, rangkain menjadi lebih ringkas, di mana kedua resistor (R1 dan R3) sudah dihubungkan secara paralel di dua sumber tegangan masing-masing dan arus juga mengalir di kedua resistor. Selanjutnya, Anda dapat menghitung besarnya arus short circuit (Ishort) dengan menggunakan hukum arus Kirchhoff, di mana Ishort = IR1 + IR2.
Selanjutnya, menerapkan hukum Ohm ke masing-masing arus cabang individu, di mana Ishort = IR1 + IR2 = VS1/R1 + VS2/R2.
Akhirnya diketahui arus yang melalui short circuit, yaitu INorton = Ishort = 30/30 + 60/60 = 1 + 1 = 2 A.
3. Lepaskan sumber daya
Untuk menemukan resistansi, Anda dapat mengganti semua sumber tegangan dengan short circuit, dan semua sumber arus diganti dengan sirkuit terbuka (open circuit).
Intinya di tahap ini, sumber tegangan diganti dengan hubung singkat (short circuit), dan sumber arus diganti dengan sirkuit terbuka (open circuit). Proses mengganti catu daya (power supply) identik dengan yang digunakan untuk teorema superposisi dan teorema Thevenin.
4. Hitung resistansi Norton
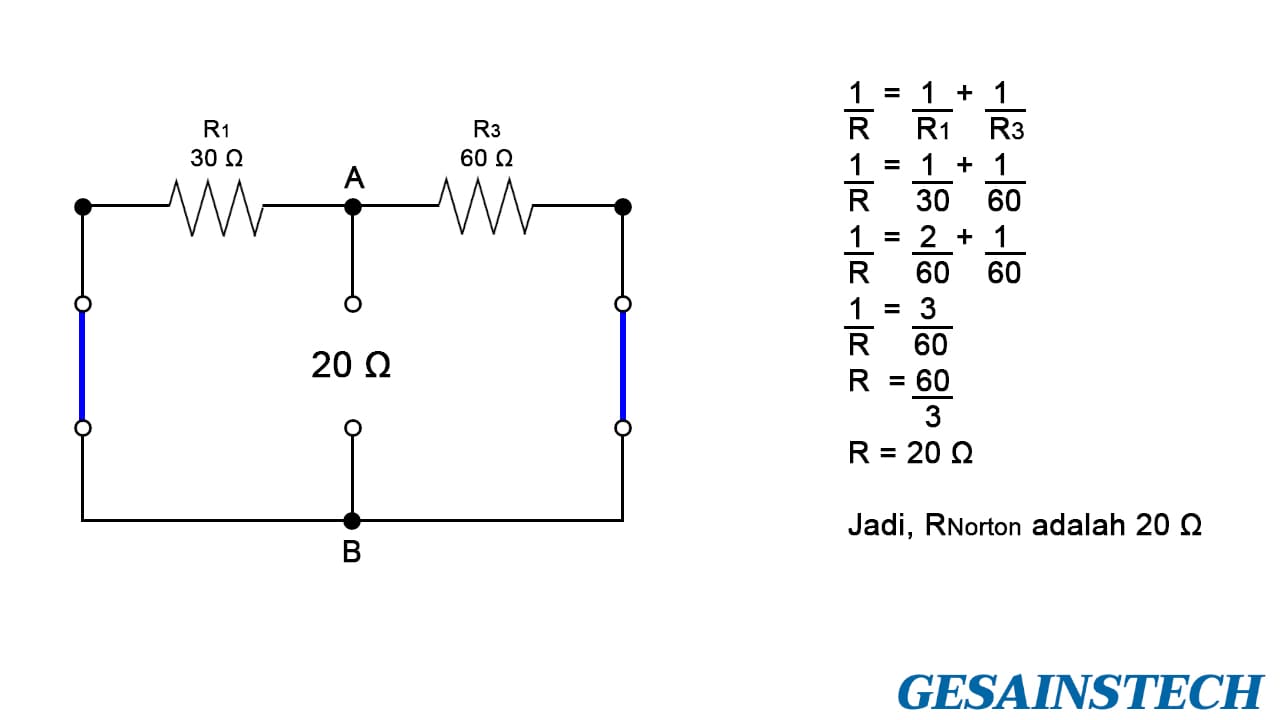
Setelah mengganti sumber tegangan dengan hubung singkat, Anda dapat mencari besarnya resistansi yang terdapat di tempat di mana beban (load) dilepas, yaitu menjumlahkan R1 dan R3 secara paralel. Lebih jelasnya amati gambar di bawah.
Jawaban 20 Ω adalah nilai dari resistansi Norton (RNorton).
5. Gambar sirkuit ekuivalen Norton
Di bawah ini adalah gambar sirkuit ekuivalen Norton, di mana Anda sudah dapat untuk melakukan perhitungan perangkat beban linier apapun yang terhubung di antara titik sambungan (terminal A dan B).
Pada gambar di atas, tepatnya yang sebelah kanan adalah sirkuit ekuivalen Norton, tetapi sudah ditambah atau diberi resistansi beban (RLoad) 120 Ω, seperti rangkaian asli (lihat langkah pertama).
6. Analisa sirkuit ekuivalen Norton
Terakhir adalah menganalisa sirkuit ekuivalen Norton terhadap beban (RLoad 120 Ω):
Kedua resistor yang dihubungkan secara paralel di terminal A dan B sehingga membuat resistansi total menjadi 17,14 Ω.
Tegangan di terminal A dan B yang sudah terhubung dengan beban menjadi 34,28 V.
Kemudian, besarnya arus listrik yang mengalir di resistor 120 Ω adalah 0,286 A.